卷积神经网络
卷积神经网络(Convolutional Neural Networks, CNN)是一类包含卷积计算且具有深度结构的前馈神经网络(Feedforward Neural Networks),是深度学习(deep learning)的代表算法之一。卷积神经网络具有表征学习(representation learning)能力,能够按其阶层结构对输入信息进行平移不变分类(shift-invariant classification),因此也被称为“平移不变人工神经网络(Shift-Invariant Artificial Neural Networks, SIANN)”
1、卷积层
卷积运算的定义如下。
1、单个卷积核:
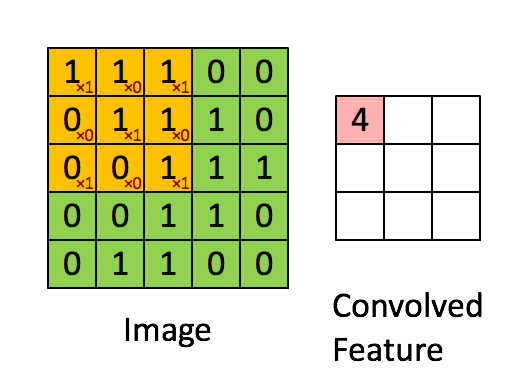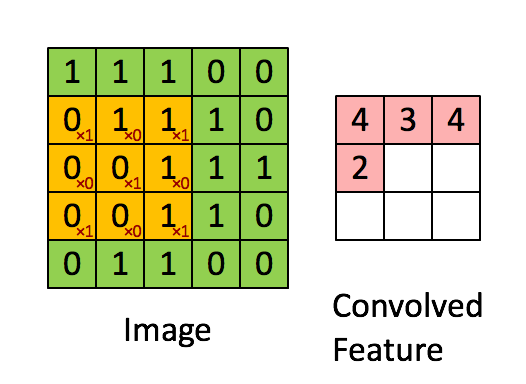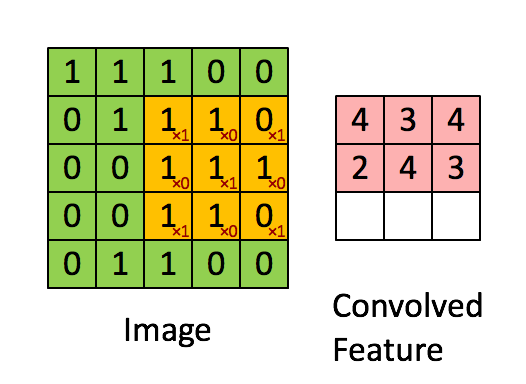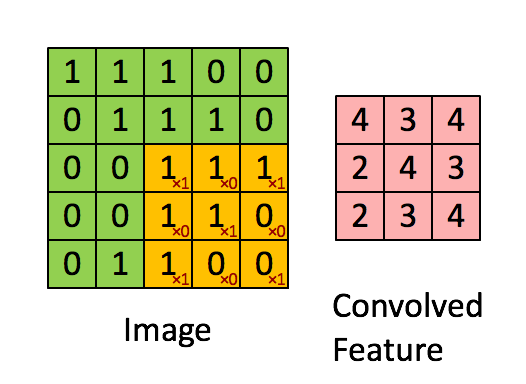
如图所示,我们有一个5x5的图像,我们用一个3x3的卷积核:
1 0 1
0 1 0
1 0 1
来对图像进行卷积操作,步长stride为1,把卷积核与对应的像素做点积,得到3x3的卷积结果。
卷积核放在神经网络里,就代表对应的权重(weight)
卷积核和图像进行点乘(dot product), 就代表卷积核里的权重单独对相应位置的Pixel进行作用
2、多个卷积核:
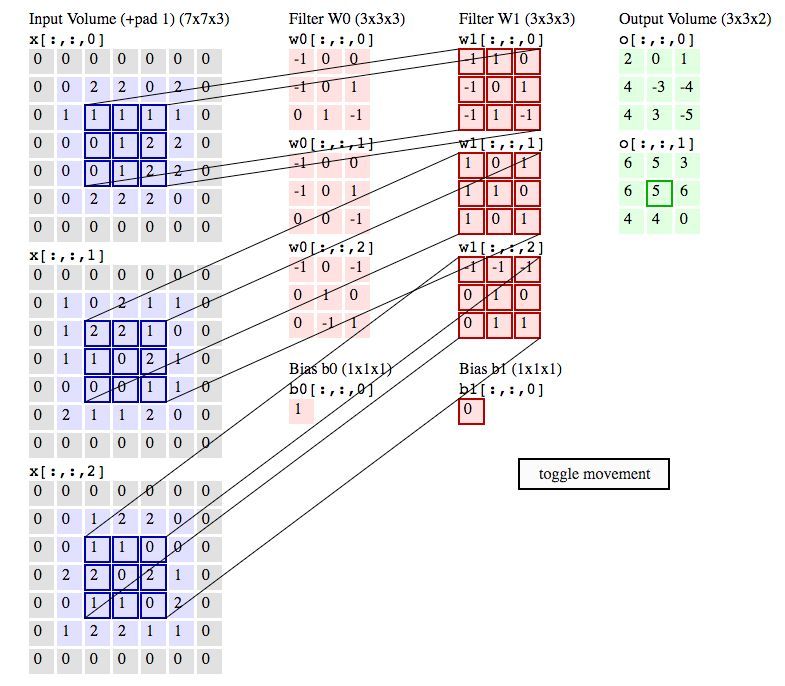
一张RGB图片,红绿蓝三个分量叠加起来产生了一张真正意义上的的图片,假设上图中的三个输入分量分别对应红绿蓝。
Filter W0,Filter W1两个过滤器(卷积核)也是三维的,分别对三个分量的进行卷积操作,再将三个输出叠加在一起形成RGB特征分量。
W1_output = 1(-1) +11+10+0(-1)+10+2*1+0(-1)+11+2(-1) =1
W2_output = 21+20+11+11+01+02+01+00+1*1=5
W3_output = 1(-1)+1(-1)+0(-1)+0*2+0(1)+02+10+11+01 = -1
Bias = 0
Final_output =W1output + W2output+W3output+bias= 1+5-1+0 = 5
总结:当卷积层获得输入图片时会先对其尺寸按照设定进行处理,然后第一个卷积核根据步长历遍整张图片中所有的像素点进行矩阵卷积运算提取特征,由此得到了输出图片的第一层,然后下一个卷积核参与到运算中,直至全部卷积核都运算结束,最后一步,把每一张输出图片叠起来的结果就是整个卷积层的输出。卷积层的主要作用:提取图像特征,参数共享,能够大幅减少计算代价。
2、激活函数
在神经元中,输入的 inputs 通过加权,求和后,还被作用了一个函数,这个函数就是激活函数。引入激活函数是为了增加神经网络模型的非线性。如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,这种情况就是最原始的感知机(Perceptron)。激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
在单层神经网络中(感知机 Perceptron),输入和输出计算关系如下: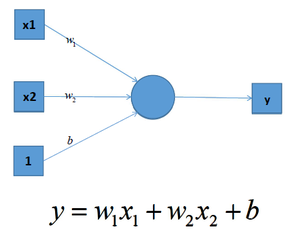
多个神经元之后,计算公式也是类似,如下图: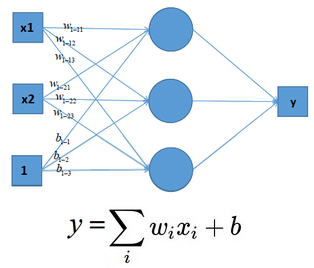
这样的模型就只能处理一些简单的线性数据,而对于非线性数据则很难有效的处理(也可通过组合多个不同线性表示,但这样更加复杂和不灵活),如下图所示: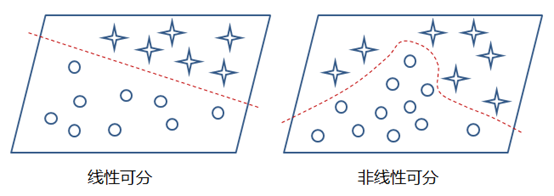
通过在神经网络中加入非线性激励函数后,神经网络就有可能学习到平滑的曲线来实现对非线性数据的处理了,如下图所示: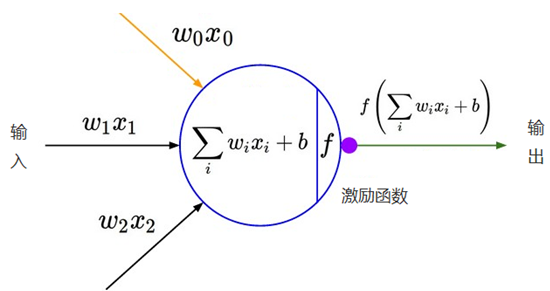
神经网络中激励函数的作用通俗上讲就是将多个线性输入转换为非线性的关系。如果不使用激励函数的话,神经网络的每层都只是做线性变换,即使是多层输入叠加后也还是线性变换。
1、Sigmoid 函数
Sigmoid函数时使用范围最广的一类激活函数,具有指数函数的形状,它在物理意义上最为接近生物神经元。其自身的缺陷,最明显的就是饱和性。从函数图可以看到,其两侧导数逐渐趋近于0,杀死梯度。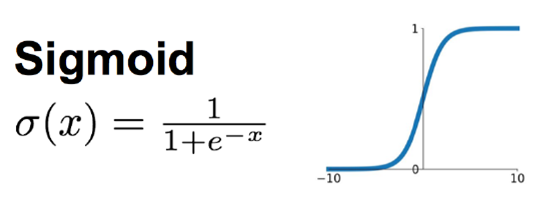
2、tanh函数
tanh是双曲函数中的一个,tanh() 为双曲正切。在数学中,双曲正切 tanh 是由双曲正弦和双曲余弦这两者基本双曲函数推导而来。正切函数时非常常见的激活函数,与Sigmoid函数相比,它的输出均值是0,使得其收敛速度要比Sigmoid快,减少迭代次数。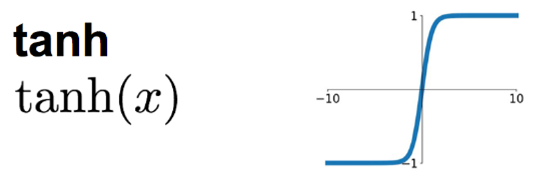
3、ReLU 函数
针对Sigmoid函数和tanh的缺点,提出ReLU函数。
线性整流函数(Rectified Linear Unit, ReLU),又称修正线性单元,是一种人工神经网络中常用的激活函数(activation function),通常指代以斜坡函数及其变种为代表的非线性函数。
最近几年比较受欢迎的一个激活函数,无饱和区,收敛快,计算简单,有时候会比较脆弱,如果变量的更新太快,还没有找到最佳值,就进入小于零的分段就会使得梯度变为零,无法更新直接死掉了。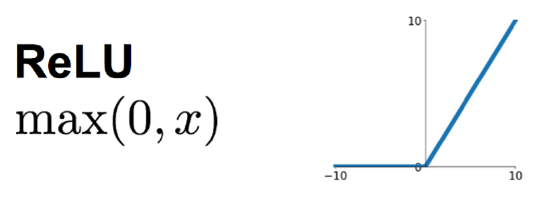
详情请见:https://www.cnblogs.com/wj-1314/p/12015278.html
3、池化层
池化(Pooling)是卷积神经网络中另一个重要的概念,它实际上是一种形式的降采样。有多种不同形式的非线性池化函数,而其中“最大池化(Max pooling)”是最为常见的。它是将输入的图像划分为若干个矩形区域,对每个子区域输出最大值。直觉上,这种机制能够有效地原因在于,在发现一个特征之后,它的精确位置远不及它和其他特征的相对位置的关系重要。池化层会不断地减小数据的空间大小,因此参数的数量和计算量也会下降,这在一定程度上也控制了过拟合。通常来说,CNN的卷积层之间都会周期性地插入池化层。
池化层通常会分别作用于每个输入的特征并减小其大小。当前最常用形式的池化层是每隔2个元素从图像划分出2*2的区块,然后对每个区块中的4个数取最大值。这将会减少75%的数据量。